第八章 并行模式:卷积 ----- 介绍常数存储器和高速缓存
8-10 章 介绍重要的并行计算模式,是很多并行算法的基础。本章是介绍卷积,以及从存储器的优化思路去优化卷积代码。
1. 卷积:
1.1 卷积并行特点:
a. 每个输出元素的计算都是相互独立的,可并行。
b. 输入元素之间具有相当程度的共享,比如核参数。
挖坑1:幽灵元素,卷积的边界缺失元素;对分块算法的复杂度和效率影响很大。
1.2 初级的卷积核函数(一维卷积):
__global__ void convolution_1D_basic_kernel(float* N, float* M, float* P, int Mask_Width, int Width){
// 参数,输入数组N,掩码数组M,结果数组P,掩码大小,输入数组大小
// 计算输入元素索引,一位卷积,网格设计为一维大小
int i = blockIdx.x * blockDim.x + threadIdx.x;
// 中间加权和变量放在 寄存器 中缓存,而不是全局变量的P中,访问速度快。
float Pvalue = 0;
// 卷积计算开始位置
int N_start_point = i - (Mask_Width / 2);
// 开始计算一次加权和
for(int j = 0; j < Mask_Width; j++){
// 边界判断,核函数内控制流产生分支,性能影响
if(N_start_point + j >= 0 && N_start_point + j < Width){
Pvalue += N[N_start_point + j] * M[j]; // **************
}
}
P[i] = Pvalue;
}问题:1. 由于幽灵元素产生if 控制流的多样性,会影响性能。但是如果大数组,小掩码,影响有限。2. 存储器带宽,可以计算 CGMA值(浮点运算和全局存储器访问的比值) = (加法和乘法两次浮点运算)/(对N 和 M的两次数据访问) = 1,非常低,下文先主要解决这个问题。
2. 常数存储器和高速缓存
观察核参数的特点:a. 尺寸小(比如常用3*3 7*7等);b. 核参数计算时数值不变;c. 所有线程都要访问,而且是以相同的顺序访问。
由上特性,优化方案为,通过将核参数M放入 常数存储器 ,利用高速缓存。先介绍常数存储器和高速缓存的特点。
2.1 常数存储器:
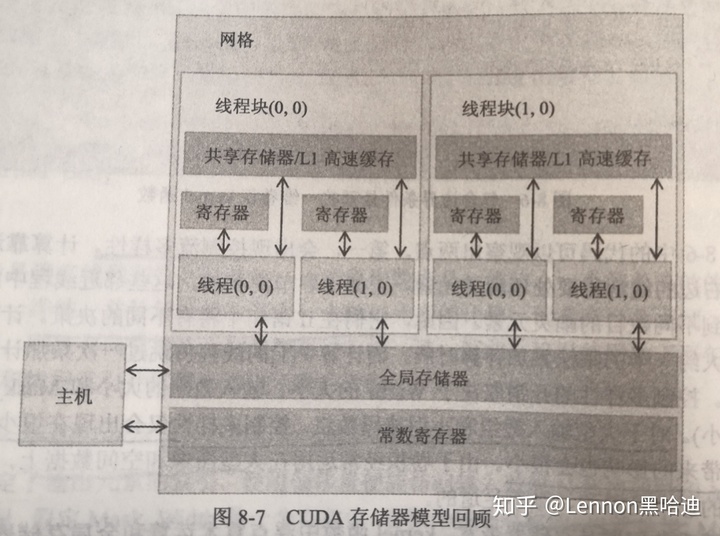
2.1.1 常数存储器特点:
与全局存储器相同都为DRAM (挖坑2);对所有线程块可见;
但在核函数执行期间,值不能被修改;
2.1.2 常数存储器容量查询方法:
cudaDeviceProp prop; // 结构体
if (cudaGetDeviceProperties(&prop, i) == cudaSuccess) {
printf("totalConstMem : %d.n", prop.totalConstMem);
}2.1.3 常数存储器变量声明:
往往声明为全局变量,与C中的全局变量性质相同。主机代码中:
#define MAX_MASK_WIDTH 10
__constant__ float M[MAX_MASK_WIDTH]; // 常量存储器变量 声明关键字为 __constant__
cudaMemcpyToSymbol(M, h_M, Mask_Width * sizeof(float)); // 此copy函数告诉CUDA,在核函数执行期间,变量值是不能改变2.1.4 优化后的代码:
__global__ void convolution_1D_basic_kernel(float* N, float* P, int Mask_Width, int Width){
// 参数,输入数组N,结果数组P,掩码大小,输入数组大小
// 注: M 采用全局变量声明,不需要参数传递
// 计算输入元素索引,一位卷积,网格设计为一维大小
int i = blockIdx.x * blockDim.x + threadIdx.x;
// 中间加权和变量放在 寄存器 中缓存,而不是全局变量的P中,访问速度快。
float Pvalue = 0;
// 卷积计算开始位置
int N_start_point = i - (Mask_Width / 2);
// 开始计算一次加权和
for(int j = 0; j < Mask_Width; j++){
// 边界判断,核函数内控制流产生分支,性能影响
if(N_start_point + j >= 0 && N_start_point + j < Width){
Pvalue += N[N_start_point + j] * M[j]; // **************
}
}
P[i] = Pvalue;
}2.1.5 解决挖坑2:
解决挖坑2,常量存储器和全局都为DRAM,为什么常量存储器中,访问速度快?
对于常数存储器中的变量,CUDA认为在核函数执行时是不变的,所以会把他们放到高速缓存中。
2.2 高速缓存:
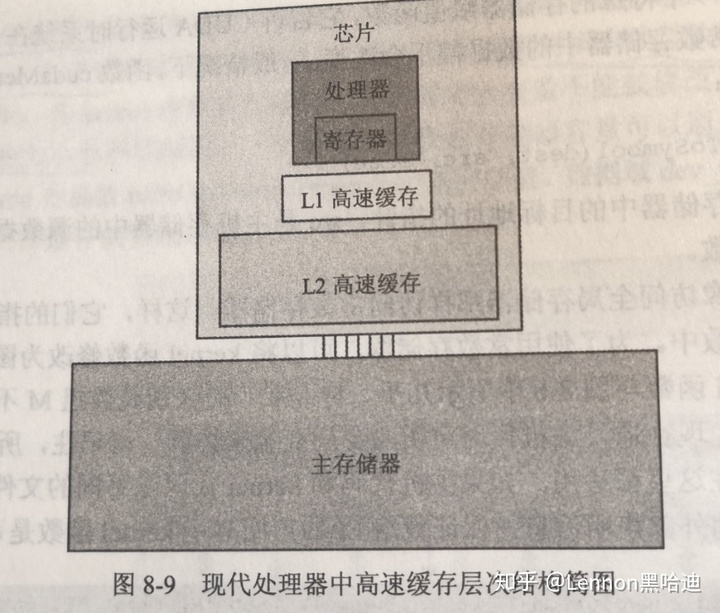
2.2.1 高速缓存的引入逻辑:
全局存储器访问一个变量,动辄数百甚至数千时钟周期,通常比算术操作慢得多,导致存储墙问题(DRAM 的长延迟和有限带宽成为几乎所有现代处理器的性能瓶颈)。为解决引入高速缓存(多级),减少访问DRAM次数。
2.2.2 高速缓存与共享存储器:
共享存储器是显式的,透明的。通过__shared__关键字声明,并显式的将全局存储器变量复制到共享存储器变量中。
高速缓存,程序只需要简单访问原始变量,不能程序显式的指定。处理器硬件自动保留一些最近或者经常使用的变量到高速缓存中,并记住他们的原始DRAM地址。当保留的变量再次被使用时,硬件会从他们的地址中判断出高速缓存中已经保留他们的副本,即可提供变量值,从而消除对DRAM的访问需求。(高速缓存还需深入)
2.2.3 多级高速缓存
速度和尺寸上的权衡。
L1 高速缓存,直接连接到处理器核心,延迟和带宽与处理器接近。通常只连接一个处理器核(挖坑3)。尺寸通常只有16KB~64KB。
L2 高速缓存,有几十个时钟周期的访问延迟。通常被多个处理器核或者CUDA设备中的多核流处理器SM共享。尺寸,128K~1M。
L3 高速缓存,几MB。
2.2.4 缓存一致性,解决挖坑3:
L1 只连接一个处理器核,导致在修改数据时,出现缓存一致性问题。缓存一致性机制保证其他处理器缓存中的数据及时更新。CPU通常支持处理器核心之间的缓存一致性。
大规模并行处理器中,实现缓存一致性是困难的,开销很大。虽然提供两级高速缓存,但是为了最大化利用硬件资源,提高算术运算吞吐率,通常不提供缓存一致性机制。
2.2.5 高速缓存和常数存储器
好在,常数存储器不修改值,不存在缓存一致性问题。硬件直接将他们放在L1高速缓存中。
缓存设计中,优化了大量线程的广播,一个warp 中访问同一个常数存储器变量时,高速缓存能为需要数据提供巨大的带宽。(ummmmmmmmm)
2.3 优化结果:
回到2.1.4 优化的代码,通过高速缓存访问M中元素,可简单假定对掩码数组的访问不会增加DRAM带宽,CGMA 提升到了2。
3. 分块一维卷积
上文是从掩码参数M入手优化的,现在对输入变量N优化代码。我们引入第五章的数据分块算法,将全局存储器中的数据复制到共享存储器中,供本线程块使用,减少DRAM的访问,提高CGMA值。
3.1 第一种分块策略

分块策略如上图。一个线程块中,将此线程块所需的所有数据都加载到共享存储器中。数据分块,由网格大小、线程块大小划分。但因为卷积算法,需要前后两个输入数组元素的值。例如分块1 第一个线程N[4]位置计算时需要N[2] N[3] 的值,所以需要把他们也加载到本线程块的共享内存。因为共享内存只在本线程块可见,所以上图N[2],N[3]既被分块0 加载到共享内存中,也会被加载到分块1的共享内存中,这类称为光环元素或边缘元素。其他的称为中间元素。
另外,如分块0左侧存在幽灵元素,分块3右侧存在幽灵元素,所以分块0 和分块3 称为 边界块。分块2 和 分块1 为 中间块 。优化代码如下:
__global__ void convolution_1D_basic_kernel(float* N, float* P, int Mask_Width, int Width){
// 参数,输入数组N,结果数组P,掩码大小,输入数组大小
// 注: M 采用全局变量声明,不需要参数传递
// 计算输入元素索引,一位卷积,网格设计为一维大小
int i = blockIdx.x * blockDim.x + threadIdx.x;
// 共享内存声明,大小为线程块大小 + 左右光环元素大小
__shared__ float N_ds[TILE_SIZE + MAX_MASK_WIDTH - 1];
// 左侧光环元素载入, 计算 光环元素 对应index, 取上一个线程块的元素
int halo_index_left = (blockIdx.x - 1)*blockDim.x + threadIdx.x;
// 光环元素,如线程块0,1,2 中的[2][3][6][7][10][11]这几个位置,进行填充
if(threadIdx.x >= blockDim.x - n){
// 把他们填充到对应共享内存数组的开头几个数中,边界填充为0
N_ds[threadIdx.x - (blockDim.x - n)] =
(halo_index_left < 0) ? 0 : N[halo_index_left];
}
// 填充中间元素, 根据线程id 找到输入数组相应位置填充
N_ds[n + threadIdx.x] = N[blockIdx.x * blockDim.x + threadIdx.x];
// 填充右侧光环元素,与填充左侧思路一致。先找到下一个线程块光环元素对应输入数组的id,
// 将他们填充到相应线程块的共享内存中
int halo_index_right = (blockIdx.x + 1)*blockDim.x + threadIdx.x;
// 光环元素,如线程块0,1,2 中的[2][3][6][7][10][11]这几个位置,进行填充
if(threadIdx.x < n){
// 把他们填充到对应共享内存数组的开头几个数中,边界填充为0
N_ds[threadIdx.x + blockDim.x + n] =
(halo_index_right >= Width) ? 0 : N[halo_index_right];
}
// 重要,栅栏同步,保证数据先复制到共享内存,才能开始下一步计算
__syncthreads();
// 中间加权和变量放在 寄存器 中缓存,而不是全局变量的P中,访问速度快。
float Pvalue = 0;
// 开始计算一次加权和
for(int j = 0; j < Mask_Width; j++){
// 从共享内存中 和 常量内存中取数,计算卷积
Pvalue += N_ds[threadIdx.x + j] * M[j];
}
P[i] = Pvalue;
}3.2 优化分析:
优化前,对数组N的访问次数为:每个线程,需要访问掩模大小的量去做加权求和。所以每个线程块就需要访问blockDim.x * Mask_Width次或者为blockDim.x * (2n + 1)。
注:对于边界块,因为存在幽灵元素,会减少访存操作次数,减少量为 n(n + 1) / 2。对于大线程块、小掩码数组来说,幽灵元素产生的影响是巨大的(猜测应该是减少量和需要访问量的比值)。
优化后,每个线程块访问数组N,加载到共享内存。加载次数为线程块大小 + 左右两侧光环元素,即 blockDim.x + 2n。
优化前与优化后访问N的比值为:
blockDim.x * (2n + 1) / blockDim.x + 2n
假设 blockDim.x = 128 n = 5时,比值为10.13;blockDim.x = 32 n = 5时,比值为8.14。可以得到结论,在使用较小线程块和分块时,访存减少的的比率可能低于预期。不过较小的分块尺寸会经常用在片上存储器容量不足的情况下,比如计算二维三维卷积时。
进一步的估算,一般 blockDim.x 会比 n 大的多,消除小项 n, 可以估计比值为,(2n + 1) 也就是掩模大小,也就是整体访存减少比率为掩码数组的大小。
3.3 另一种分块一维卷积
此优化思路的依据是,GPU提供 L1 L2 高速缓存。L1 为每个SM私有的,L2 为所有SM共享的。存在一个事实是:光环元素可能会存在L2 缓存中。比如 线程块1 使用光环元素时,因为之前线程块0 访问而存储到L2上了,这样线程块1 访问光环元素时,直接访问L2 而不是 DRAM了。所以本优化思路是只将中间元素存储到共享内存中,光环元素直接去访问原始输入数组了。
__global__ void convolution_1D_basic_kernel(float* N, float* P, int Mask_Width, int Width){
// 参数,输入数组N,结果数组P,掩码大小,输入数组大小
// 注: M 采用全局变量声明,不需要参数传递
// 计算输入元素索引,一位卷积,网格设计为一维大小
int i = blockIdx.x * blockDim.x + threadIdx.x;
// 共享内存声明,大小只是线程块大小了, 相比上节,无左右光环元素大小
__shared__ float N_ds[TILE_SIZE];
// 只需要填充中间元素即可
N_ds[threadIdx.x] = N[i];
// 重要,栅栏同步,保证数据先复制到共享内存,才能开始下一步计算
__syncthreads();
// 本线程中, 共享内存中取数相对N的 开始和结尾idx,用于判断 数是从共享取,还是DRAM
int This_tile_start_point = blockIdx.x * blockDim.x;
int Next_tile_start_point = (blockIdx.x + 1) * blockDim.x;
// 卷积计算的开始 idx,是相对于N 中的idx
int N_start_point = i - (Mask_Width / 2);
// 中间加权和变量放在 寄存器 中缓存,而不是全局变量的P中,访问速度快。
float Pvalue = 0;
// 开始计算一次加权和
for(int j = 0; j < Mask_Width; j++){
// 本轮卷积加权和计算的 取数idx 相对于N输入数组,
int N_index = N_start_point + j;
// 保证不是幽灵元素
if(N_index >= 0 && N_index < Width){
// 如果说在共享内存中,从共享内存中取
if(N_index >= This_tile_start_point && N_index < Next_tile_start_point){
Pvalue += N_ds[threadIdx.x + j - (Mask_Width / 2)] * M[j];
} else{
// 如果不在共享内存中,从N中取
Pvalue += N[N_index] * M[j];
}
}
}
P[i] = Pvalue;
}